Linear Models

import numpy as np
import matplotlib.pyplot as plt
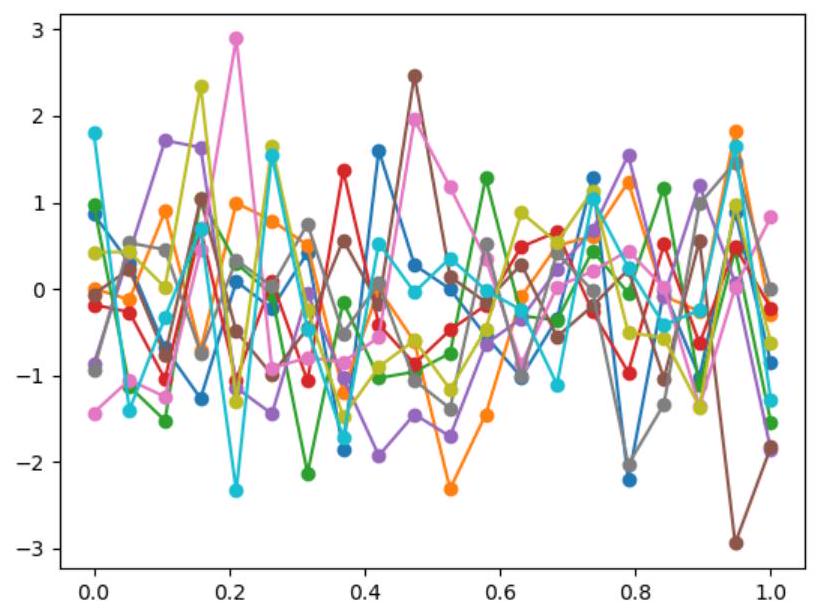
def plot_unit_gaussian_samples(D):
p = plt.figure()
xs = np.linspace(0, 1, D)
for color in range(10): # 10 for 10 curves
ys = np.random.multivariate_normal(np.zeros(D), np.eye(D))
plt.plot(xs, ys)
return p
plot_unit_gaussian_samples(20)
def kernel(X1,X2):
Sigma = np.empty((X1.shape[0],X2.shape[0]))
for i in range(X1.shape[0]):
for j in range(X2.shape[0]):
Sigma[i,j] = np.exp(-(X1[i]-X2[j])**2/2)
return Sigma
def mean(X):
Mu = np.zeros(X.shape[0]) #np.mean(X,axis=0)
return Mu
import numpy as np
import matplotlib.pyplot as plt
# Input
def input_fun(X):
Coefs = np.array([6,-2.5,-2.4,-0.1,0.2,0.03])
y = np.sum(np.tensordot(X , np.ones(Coefs.size), axes=0 )** np.arange(Coefs.size) * Coefs,axis=1)
return y
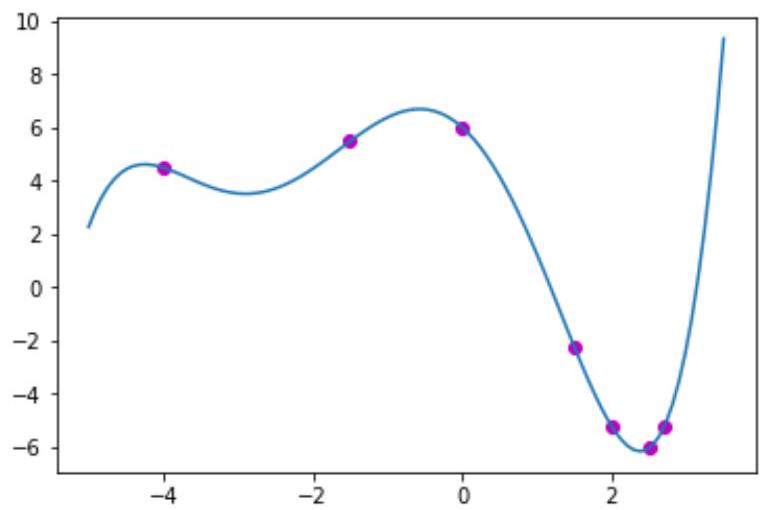
X_true = np.linspace (-5,3.5,100)
y_true = input_fun(X_true)
plt.plot(X_true,y_true)
X_train = np.array([-4,-1.5,0,1.5,2,2.5,2.7])
y_train = input_fun(X_train)
plt.figure(1)
plt.scatter(X_train,y_train,color='m')
# Kernel
def kernel(X1,X2):
# Sigma = np.exp(-(X1.reshape(X1.shape[0],-1) - X2)**2/2)
Sigma = np.empty((X1.shape[0],X2.shape[0]))
for i in range(X1.shape[0]):
for j in range(X2.shape[0]):
Sigma[i,j] = np.exp(-(X1[i]-X2[j])**2/2)
return Sigma
def mean(X):
Mu = np.zeros(X.shape[0]) #np.mean(X,axis=0)
return Mu
Sigma = kernel(X_train,X_train)
Mu = mean(X_train)
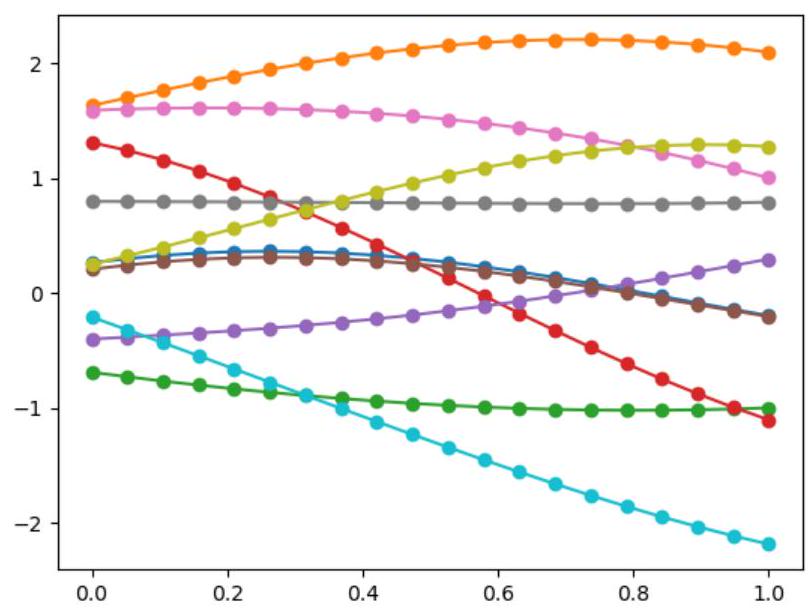
# Sampling for showing the Gaussian samples
Sigma_sampling = kernel(X_true,X_true)
Mu_sampling = mean(X_true)
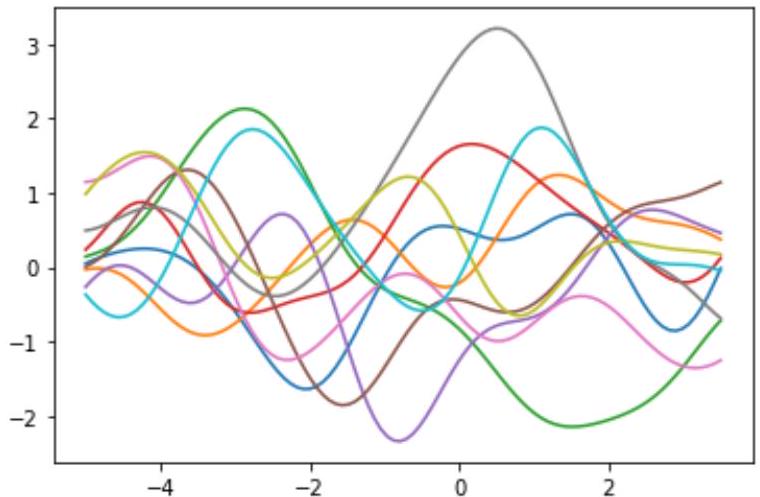
for n_sampling in range(10):
Y_sample = np.random.multivariate_normal(Mu_sampling,Sigma_sampling) #with smoothing (Sigma with
kernel)
plt.figure(2)
plt.plot(X_true,y_sample)
Y_sample = np.random.multivariate_normal(Mu_sampling,np.eye(Mu_sampling.shape[0])) #without
smoothing (Sigma without kernel)
plt.figure(0)
plt.plot(X_true,y_sample)
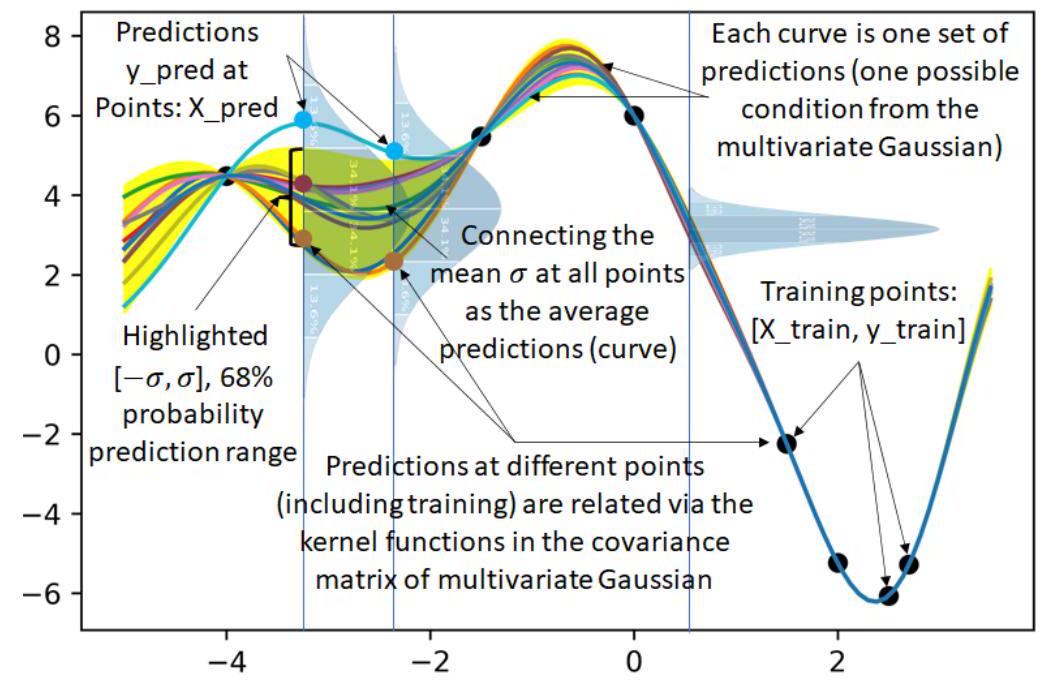
# Prediction
X_pred = X_true
K_whole = kernel(np.hstack((X_train,X_pred)),np.hstack((X_train,X_pred))) # Sigma matrix for the
combined Gaussian distribution of [X_train, X_pred]
K = K_whole[0:X_train.shape[0],0:X_train.shape[0]]
K_ast = K_whole[:X_train.shape[0],X_train.shape[0]:]
K_ast_ast = K_whole[X_train.shape[0]:,X_train.shape[0]:]
M = Mu
M_ast = mean (X_pred)
Mu_pred = M_ast + ( K_ast.T @ np.linalg.inv(K) @ (y_train - Mu).reshape((y_train.size,1)) ).reshape(
M_ast.size)
Sigma_pred = K__ast_ast - K_ast.T @ np.linalg.inv(K) @ K_ast
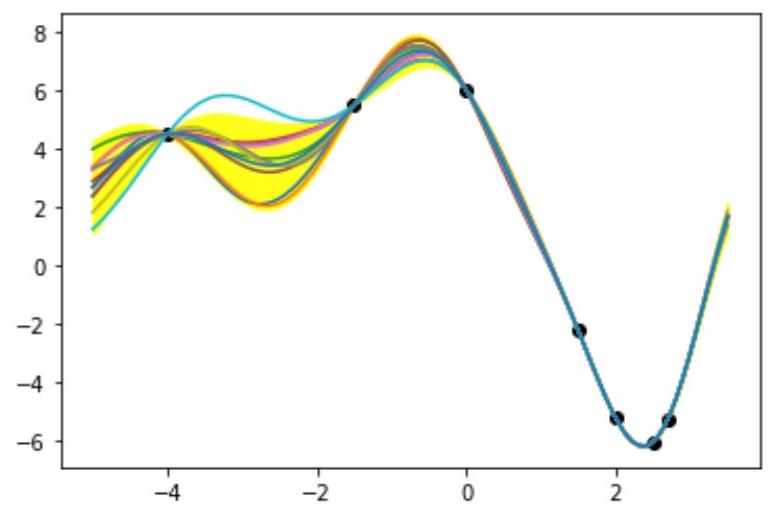
plt.figure(3)
for n_sampling_pred in range(10):
y_pred = np.random.multivariate_normal(Mu_pred,Sigma_pred)
plt.plot(X_pred,y_pred) # Plot n (number of iterations) predicted curves
plt.plot(X_pred,Mu_pred) # Predict average prediction
# sigma = np.std(X_pred) # Incorrect
sigma = Sigma_pred.diagonal()**0.5 # Correct
plt.fill_between(X_pred,Mu_pred-2*sigma,Mu_pred+2*sigma,color='yellow',alpha=0.9) # Show the region
with mu +- sigma (68%) (2*sigma is 95%, 3*sigma is 99.7%)